Base 2 4 8
The reason computers use the base-2 system is because it makes it a lot easier to implement them with current electronic technology. You could wire up and build computers that operate in base-10, but they would be fiendishly expensive right now. On the other hand, base-2 computers are relatively cheap.
Each radix 4, 8 and 16 is a power of 2, so the conversion to and from binary is implemented by matching each digit with 2, 3 or 4 binary digits, or bits. For example, in base 4, 230210 4 = 10 11 00 10 01 00 2. Since 16 is a power of 4, conversion between these bases can be implemented by matching each hexadecimal digit with 2 quaternary digits. Instant free online tool for base-10 to base-8 conversion or vice versa. The base-10 to base-8 conversion table and conversion steps are also listed. Also, explore tools to convert base-10 or base-8 to other numbers units or learn more about numbers conversions.

- Evaluate log base 2 of 1/4. Rewrite as an equation. Rewrite in exponential form using the definition of a logarithm. If and are positive real numbers and does not equal, then is equivalent to. Create equivalent expressions in the equation that all have equal bases.
- The octal numeral system, or oct for short, is the base-8 number system, and uses the digits 0 to 7.Octal numerals can be made from binary numerals by grouping consecutive binary digits into groups of three (starting from the right). For example, the binary representation for decimal 74 is 1001010.
- Base conversion calculator with steps: binary,decimal,octal,hex conversion.
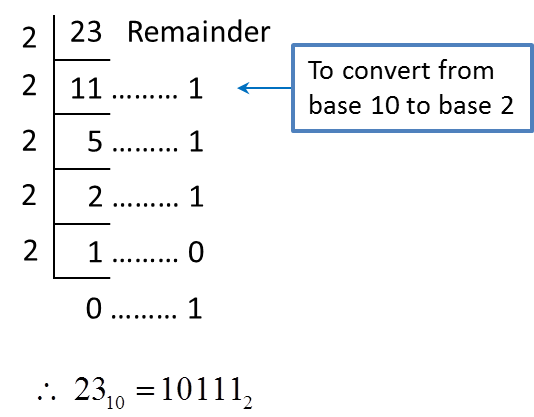
So computers use binary numbers, and therefore use binary digits in place of decimal digits. The word bit is a shortening of the words 'Binary digIT.' Whereas decimal digits have 10 possible values ranging from 0 to 9, bits have only two possible values: 0 and 1. Therefore, a binary number is composed of only 0s and 1s, like this: 1011. How do you figure out what the value of the binary number 1011 is? You do it in the same way we did it above for 6357, but you use a base of 2 instead of a base of 10. So:
Advertisement
Advertisement
(1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (1 * 2^0) = 8 + 0 + 2 + 1 = 11
You can see that in binary numbers, each bit holds the value of increasing powers of 2. That makes counting in binary pretty easy. Starting at zero and going through 20, counting in decimal and binary looks like this:
Base 2 4 8 X 8
When you look at this sequence, 0 and 1 are the same for decimal and binary number systems. At the number 2, you see carrying first take place in the binary system. If a bit is 1, and you add 1 to it, the bit becomes 0 and the next bit becomes 1. In the transition from 15 to 16 this effect rolls over through 4 bits, turning 1111 into 10000.
Bits are rarely seen alone in computers. They are almost always bundled together into 8-bit collections, and these collections are called bytes. Why are there 8 bits in a byte? A similar question is, 'Why are there 12 eggs in a dozen?' The 8-bit byte is something that people settled on through trial and error over the past 50 years.
With 8 bits in a byte, you can represent 256 values ranging from 0 to 255, as shown here:
In the article How CDs Work, you learn that a CD uses 2 bytes, or 16 bits, per sample. That gives each sample a range from 0 to 65,535, like this:
Base 24 Math
Next, we'll look at one way that bytes are used.